三角公式整理 特殊三角函数值万能公式 附函数值表 学习岛
三角比・三角関数の公式一覧。 正弦・余弦・加法定理など Tooda Yuuto 17年7月3日 / 21年6月2日 このページでは、 三角比・ 三角関数 の公式 をまとめています。 予習・復習に役立てていただければ嬉しいです。 スポンサーリンク 目次 sinθ・cosθ・tanθの 171 勾股定理(通用)说课稿一等奖 171 勾股定理 初中数学 人教11课标版 勾股定理是九年制义务教育教科书八年级下册第十七章的内容,是几何中几个重要定理之一,它揭示的是直角三角形中三边的数量关系。 它在数学的发展中起过重要的作用,在现时
三角定理 表
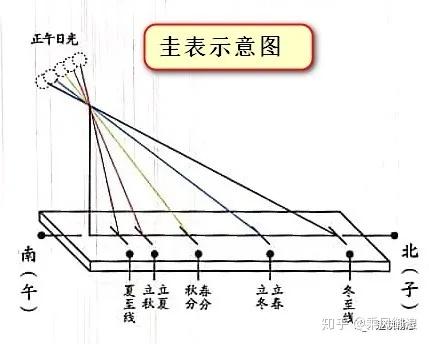
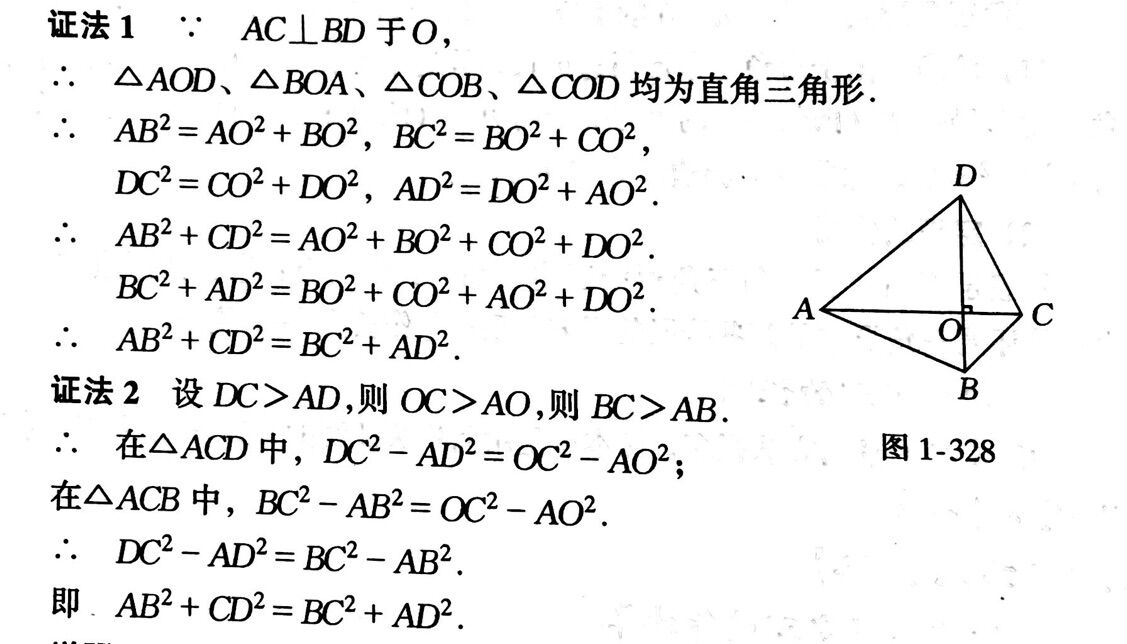
三角定理 表-直角三角 形の底辺と高 高校の数学の三角関数表ではこのような小さな角を求めることができないので、たいへん助かりました。 ピタゴラスの定理は知っていても、角度の計算となるとわからなく、縮小の図を描いて分度器で計算しようとしましたが 1 勾股定理(毕达哥拉斯定理)2 射影定理(欧几里得定理)在rt abc中,∠acb=90°,cd是斜边ab上的高,则有射影定理如下:①cd2=ad·db②bc2=bd·ba③ac2=ad·ab④ac·bc=ab·cd(等积式,可用面积来证明)3 三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4
三角函数数值表0 三角函数表值查表0 360 柏然网
三角関数の加法定理 1 コインをn回投げたとき、表が3回連続で出ないような場合の数を$ a_n $とする。 この時の漸化式を教えてください。自然 2 1/0の答えが0じゃなく無しになるのはなぜですか? 0/1や0×1の答えは0なのに 以下の文書は次の翻訳です。 History of trigonometry Wikipedia (三角法の歴史) プトレマイオスは「太陽の黄経から、太陽の赤緯と赤経」を求めるために 球面三角法を使用していますが、現代の三角法では直接これが可能ではないかと思い、 確かめたものが訳注 2 です。数学授業プリント(高校) 21年8月1日 LuaLaTeXプリントを3枚追加, 21年2月11日 プリントを1枚追加, 21年2月6日 プリントを1枚追加, 年12月13日 プリントを2枚追加, 11月28日 プリントを1枚追加, 11月14日 プリントを3枚追加, 8月9日 プリントを1枚追加, 5月31日
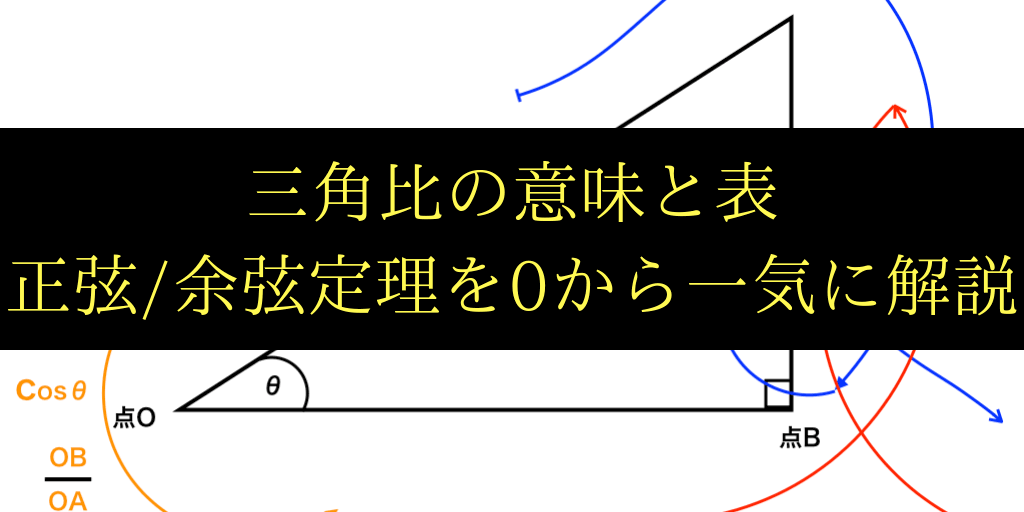
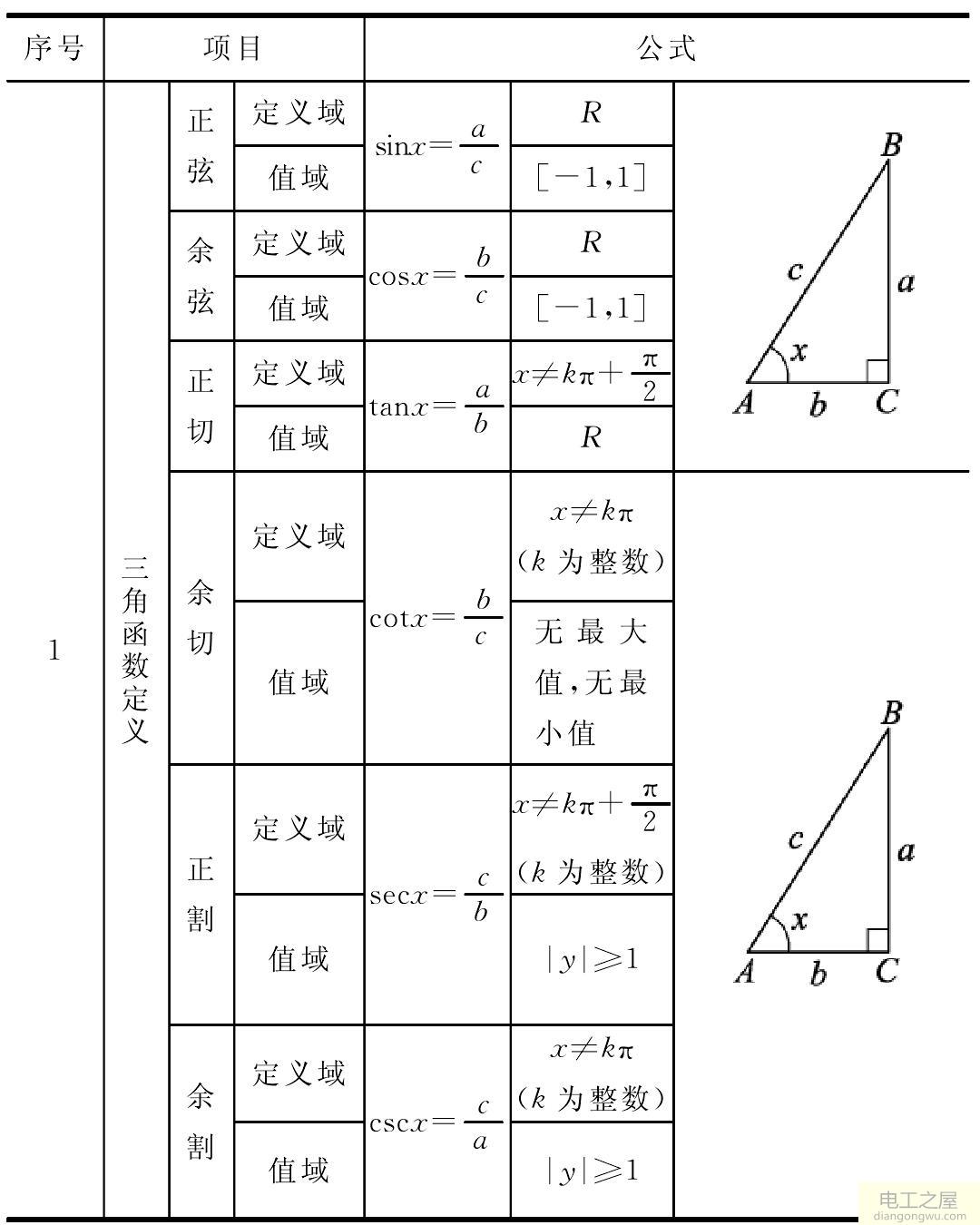
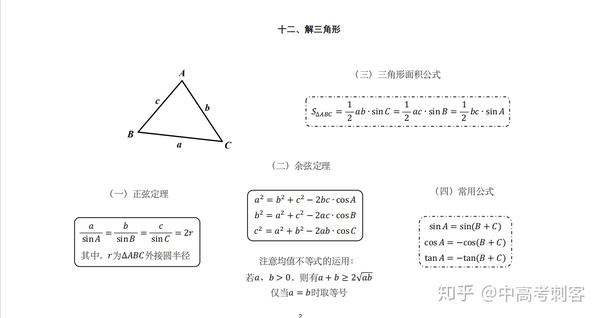
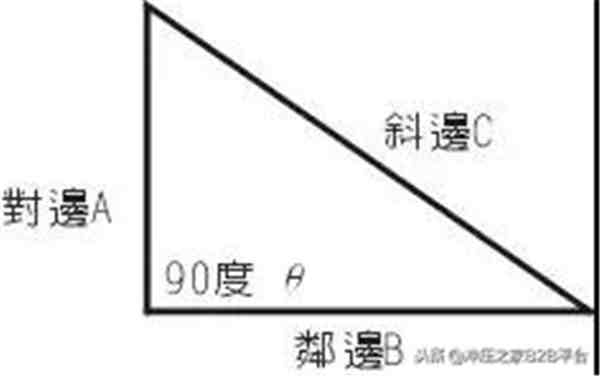
< 正弦定理1 > 三角形abc で,頂点a, b, c に対する辺の長さ を,それぞれ,a, b, c とする。また∠a, ∠b, ∠c の 大きさを,それぞれa, b, c と書くことにする。 このとき次の定理が成立する。 ここでr は三角形abc の外接円の半径である。 証明 外接円の中心をo と 三角比については、以下の記事で詳しく説明しています。 三角比 (サイン コサイン タンジェント) とは?定義と相互関係 三角比・三角関数の代表的な値は頭に定着させておきましょう! 三角比の表・三角関数表(sin cos tan の値)の一覧! 三角比の定義三角関数から求められる versine, coversine, haversine, exsecant などの各関数は、かつて測量などに用いられた。例えば haversine は球面上の2点の距離を求めるのに使用された。haversineを使用すると関数表の表をひく回数を減らすことができるからである。
三角定理 表のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 | ||
「三角定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「三角定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
「三角定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
「三角定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「三角定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  |  |
「三角定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 | ||
「三角定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
「三角定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
「三角定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
「三角定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
「三角定理 表」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |
三角関数の公式の覚え方と導出のコツ一覧 (丸暗記不要) 三角関数の公式を最小限の記憶 (加法定理)と、"加法定理から全ての公式を導く方法"をインプットしておくことで、覚える量を激減させるだけでなく、試験中に忘れるといった心配も無くなりますコラム 三角関数表(難易度2) 三角関数 は直角三角形に対して考えられる6種類の比の間の関係を扱う 三角法 がその起源で、角度に比の値を対応させる6種類の関数です。 三角法は英語ではtrigonometry といい、三角形の測量という意味です。 四千年前の





0 件のコメント:
コメントを投稿